Rank

Table of contents

• 1. Rank-Nullity Theorem (Dimension Theorem)
• 2. The Four Fundamental Subspaces ★★★
• 3. properties
• 4. Incidence Matrix in Graph Theory

---

1. Rank-Nullity Theorem (Dimension Theorem)

\[A : m \times n\] \[\text{rank}(A) + \text{nullity}(A) = n\] \[\text{dim }C(A^T) + \text{dim }N(A) = n\]

or

\[f : V \rightarrow W\] \[\text{dim} V = \text{dim Im} f + \text{dim Ker} f\]

2. The Four Fundamental Subspaces ★★★

\[A \mathbf{x} = \mathbf{0}\] \[\rightarrow (\text{ith row of }A) \cdot x = 0 \rightarrow \forall \text{row of }A \perp \forall x \in N(A)\] \[\rightarrow C(A^T) \perp N(A)\] \[\rightarrow C(A) \perp N(A^T)\]

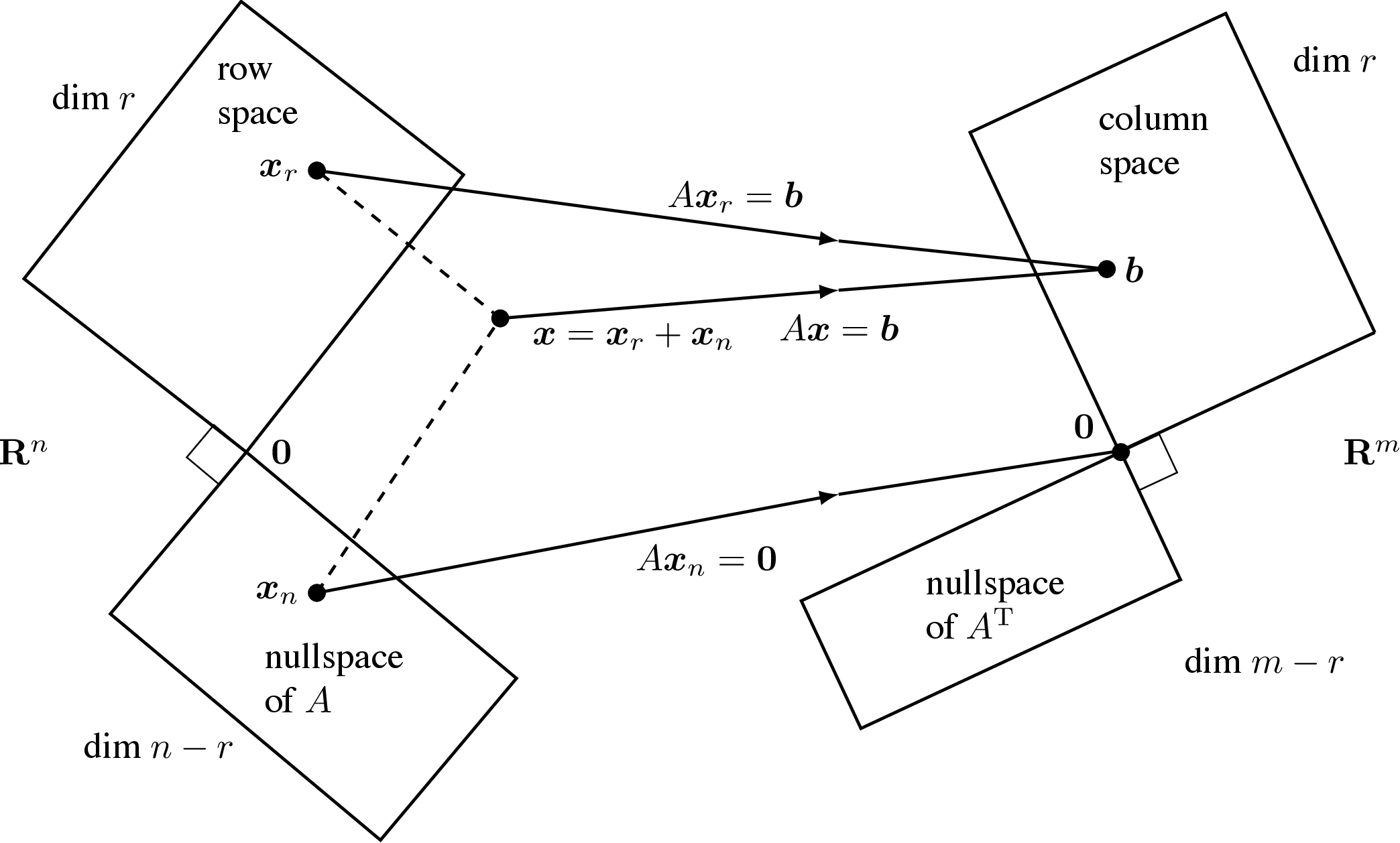
3. properties

1. $\text{rank}(AB) \le \text{rank}(A), \quad \text{rank}(AB) \le \text{rank}(B)$
2. $\text{rank}(A+B) \le \text{rank}(A) + \text{rank}(B)$
3. $\text{rank}(AA^T) = \text{rank}(A^TA) = \text{rank}(A) = \text{rank}(A^T)$
4. $\text{rank}(AB)=r$   if   $ A_{ m \times r}, B_{ r \times n}$ has same $\text{rank}=r$ ★★★
   • $\text{rank}(AB) \ne \text{rank}(BA)$

4. Incidence Matrix in Graph Theory

---