Boosting (decrease bias) : Several sequential weak learners build a strong learner.
Table of contents
- 1. What is Boosting
- 2. Strong and Weak Learner : Statistical Learning Theory
- 3. AdaBoost : Adaptive Boosting
- 4. Gradient Tree Boosting
- 5. XGBoost
1. What is Boosting
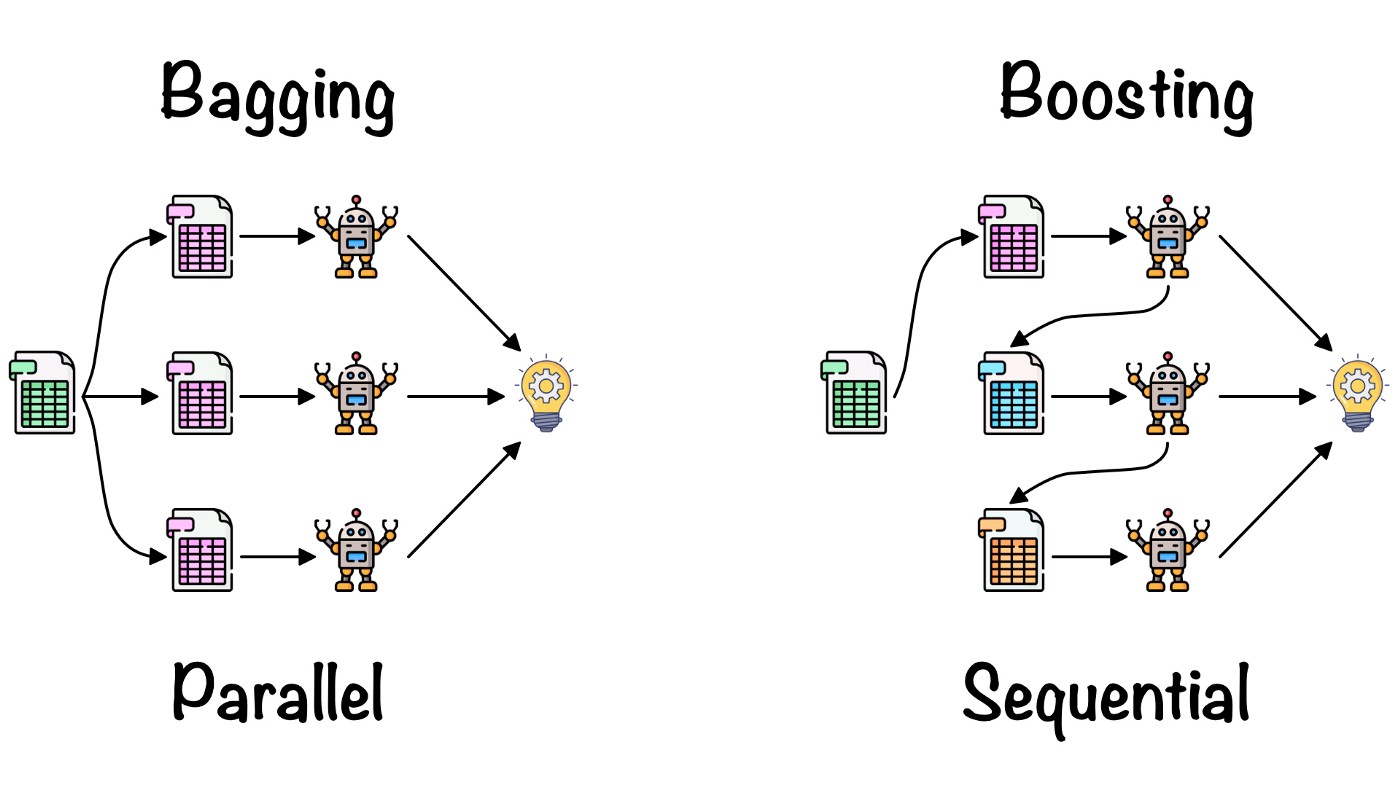 |
|---|
| Comparison of bagging and boosting (Source) |
Motivation
Humans learn from their mistakes and try not to repeat them futher in life. (Source)
Central idea
implement of homogeneous ML algorithms in a sequential way, where each of these ML algorithms tries to improve the stability of the model by focusing on the errors made by the previous ML algorithm (Source)
The way of focusing on the predecessor’s error is the key to distinguish between variations of the boosting technique.
2. Strong and Weak Learner : Statistical Learning Theory
Roughly speaking, Weak Learner refers to simple models that do only slightly better than random chance. (Source)
Notation
| $\mathcal{X}$ | an input space |
| $\mathcal{Y}$ | an output space |
| $\mathcal{D}$ | and unknown distribution on $\mathcal{X} \times \mathcal{Y}$ |
| $\ell : \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}$ | a loss function |
| $(x_i, y_i) \in \mathcal{X} \times \mathcal{Y}$ | the i-th sample from $\mathcal{D}$ |
| $h : \mathcal{X} \rightarrow \mathcal{Y}$ | a hypothesis |
| $\mathcal{H}$ | hypothesis class/space/set : the set of all possible hypothesis |
| $\text{err}_{\mathcal{D}}(h)$ | generalization error of $h$ |
Then, in formally notation,
\[\text{arg} \min_h L_{\mathcal{D}}(h) = E_{(x,y) \sim \mathcal{D}} \Big[ \ell \big( h(x), y \big) \Big]\]is the goal of a machine learning : find a model $h$ closed to $\mathcal{D}$
(?) Definition Strong Learnability of $\mathcal{H}$
$\mathcal{H}$ is strongly learnable if there is an algorithm that
for $\forall \mathcal{D}$, $\forall \epsilon > 0$, $\forall \delta > 0$, uses $\text{poly} \Big( \dfrac{1}{\epsilon}, \dfrac{1}{\delta}, VC(\mathcal{H}) \Big)$ samples from $\mathcal{D}$ and returns a classifier $h$ such that
The algorithm performing this learning task is call a strong learner.
(?) Definition Weak Learnability of $\mathcal{H}$
$\mathcal{H}$ is $\gamma$-weakly learnable if there is an algorithm that
for $\forall \mathcal{D}$, $\forall \delta > 0$, uses $\text{poly} \Big( \dfrac{1}{\delta}, VC(\mathcal{H}) \Big)$ samples from $\mathcal{D}$ and returns a classifier $h$ such that
The algorithm performing this learning task is call a $\gamma$-weak learner.
(cf)
3. AdaBoost : Adaptive Boosting
(0) algorithm
- AdaBoost makes a sequence of weak learners (e.g. decision stumps).
- Each weak learner is made based on weighted samples from the dataset, and evaluated its performance to be used as a weight.
- When predicting after learning, the prediction follows the weighted voting/average of the decisions of each learner.
(1) AdaBoost.M1 : binary classification
Input:
- learning dataset $\lbrace (x_i, y_i) \rbrace_m \in \mathcal{X} \times \mathcal{Y}$ with size $m$, where $\mathcal{Y} = \lbrace -1, +1 \rbrace$ (binary classification)
- $T$ : the number of boosting round (the number of hypotheses)
- $\eta \in \mathbb{R}$ : the learning rate (defalut : $1$)
Initialize:
- $\mathcal{D}_1(i) \equiv \dfrac{1}{m}$
where $\mathcal{D}_t$ is a distribution such that $\mathcal{D}_t(i)$ is the weight of i-th sample $(x_i, y_i)$ at iteration $t$
For $t = 1, 2, \cdots, T$ :
- Train the $t$-th weak learner $h_t : \mathcal{X} \rightarrow \mathcal{Y}$ with the data distribution $\mathcal{D}_t$
(choose the best $h_t$) - Compute the learner weight $\alpha_t = \dfrac{1}{2} \text{log} \dfrac{1- \epsilon_t}{\epsilon_t}$
where $\let\sb_$ $\epsilon_t = \sum\limits_{i} \mathcal{D}\sb{t} (i) \cdot \text{I}_{(h_t(x_i) \ne y_i)}$ : sum of weight of samples predicted wrong - Update $\mathcal{D}\sb{t+1}(i) = \mathcal{D}\sb{t}(i) \cdot \dfrac{\text{exp} \big( - \eta \alpha_{t} y_{i} h_{t} (x_{i}) \big)}{Z_{t}}$
where $Z_{t}$ is a normalizer to make $\mathcal{D}\sb{t+1}$ also a distribution
Output: the final hypothesis $H(x)$ :
\[H(x) = \text{sign} \left( \sum_{t=1}^T \alpha_t h_t(x) \right) \in \mathcal{Y} = \lbrace -1, +1 \rbrace\]explanation
how to train $h_t$ and choose the best? (Source) (Source)
why $\alpha_t$ is the learner weight? (Source)
Note that
\[Z_t \cdot \mathcal{D}_{t+1}(i) = \mathcal{D}_{t}(i) \cdot e^{\pm \eta \alpha_t} = \begin{cases} \mathcal{D}_{t}(i) \cdot e^{+ \eta \alpha_t}, & \text{if } y_i = h_t(x_i) \text{ : predict correctly}\\ \mathcal{D}_{t}(i) \cdot e^{- \eta \alpha_t}, & \text{if } y_i \ne h_t(x_i) \text{ : predict wrong} \end{cases}\]