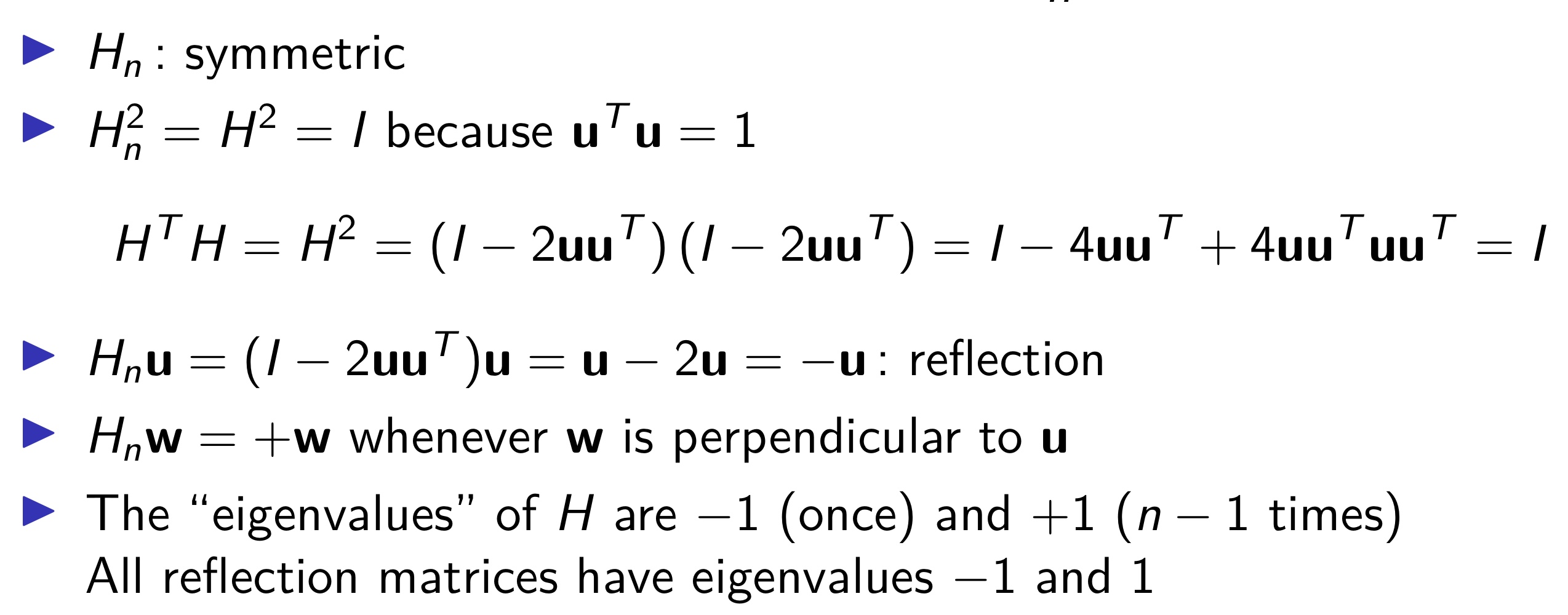Special Matrix

Table of contents

• 0. Symmetric Matrix
• 1. Orthogonal Matrix
• 2. Hadamard Matrix (아다마르 행렬)
• 3. Projection Matrix → Least Square Error
• 4. Rotation and Reflection
• 5. Householder Matrix

---

0. Symmetric Matrix

1. Properties
   • $\forall \lambda$ : real
   • $\exists \lbrace x_i \rbrace$ : orthonormal and full (spans $V$). ($\implies$ diagonalizable : spectral thm. )
2. Spectral Theorem

\[S = Q \Lambda Q^T\]

1. Orthogonal Matrix

: transpose rather than inverse

1. Rectangular $Q$ : tall thin matrix with orthonormal columns ($m \times n, m \gt n$)

\[Q^TQ = I_n\] \[QQ^T = \begin{bmatrix} I_n & O\phantom{_{m-n}} \\ O & O_{m-n} \end{bmatrix} \ne I_m\] \[\forall \mathbf{x}, \lVert Q\mathbf{x} \rVert = \lVert \mathbf{x} \rVert\]

1. Definition (Orthonomal Matrix)
   • $Q$ : square matrix with orthonormal columns ($n \times n$)
2. iff conditions
   • $Q^TQ = QQ^T = I_n$
3. Properties
   • $Q_1, Q_2 \text{ : orthogonal} \implies Q_1Q_2 \text{ : orthogonal}$
   • $ \lVert Q\mathbf{x} \rVert = \lVert \mathbf{x} \rVert $ : isometry
   • orthogonal $\implies$ rotation

2. Hadamard Matrix (아다마르 행렬)

1. Definition, notation
   • $H_n$ : entries are $\pm 1$, and rows/columns are mutually orthogonal.
2. Properties
   • $H_n$ is not orthogonal. (scalar multipled orthogonal matrix)
3. Hadamard Conjecture
   • $H_n$ exists iff $n \equiv 0 (\text{mod } 4)$

3. Projection Matrix → Least Square Error

\[P : R^n \xrightarrow{\text{proj}} C(P)\] \[P : \mathbf{b} \mapsto P\mathbf{b}\]

1. Definition
   • $P$ : square matrix $s.t.$ $P^2=P$ : idempotent
   • “projection twice = projection once”
2. Definition (Orthogonal Projection Matrix)
   • $P^2 = P = P^T$ : idempotent and symmetric

\[\begin{align*} P^2 = P = P^T &\iff \forall \mathbf{v}, \ P^T\mathbf{v} = P\mathbf{v} = P^2\mathbf{v} \\ &\implies \forall \mathbf{v}, \ P^T(\mathbf{v}-P\mathbf{v}) = P(\mathbf{v}-P\mathbf{v}) = P\mathbf{v}-P^2\mathbf{v} = \mathbf{0} \\ &\iff \forall v \forall p_i, \ p_i \cdot (\mathbf{v}-P\mathbf{v}) = 0 \\ &\iff \forall v, \ \forall p_i \perp (\mathbf{v}-P\mathbf{v}) \\ &\iff C(P) \perp (\mathbf{v}-P\mathbf{v}) \\ &\iff P\mathbf{v} \text{ is an orthogonal projection of } \mathbf{v} \text{ on } C(P) \end{align*}\]

4. Rotation and Reflection

\[Q_{\text{rotate}} = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & \ \ \ cos\theta \end{bmatrix} \text{ : rotate } \theta \quad\] \[Q_{\text{reflect}} = \begin{bmatrix} cos2\theta & \ \ \ sin2\theta \\ sin2\theta & -cos2\theta \end{bmatrix} \text{ : rotate } \pi + 2\theta\]

• rotation $\times$ rotation : rotation
• reflection $\times$ reflection : rotation
• rotation $\times$ reflection : reflection

5. Householder Matrix

\[H_n = I_n - 2\mathbf{u}\mathbf{u^T}\]

where $\mathbf{u}$ is a unit vector

• Properties :
  

---