Bagging (decrease variance) : Bootstrapping + Aggregating
Table of contents
- 1. What is Bagging?
- 2. Statistics - variance reduction
- 3. Advantages vs Disadvantages
- 4. Random Forest : a representative bagging model
1. What is Bagging?
- Bootstrapping : generate new traing sets by uniformly sampling with replacement from the standard traing set
(cf) bootstrap (n.) : better oneself by rigorous, unaided effort (Source) - Aggregating : aggregate the results of multiple models.
- (ex) Random Forest
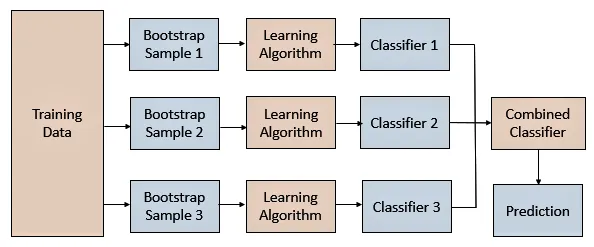 |
|---|
| bagging flow. (Source) |
2. Statistics - variance reduction
Proof
Let $X_1, X_2, \cdots, X_n$ be samples from identical distribution with a variance $\sigma^2$.
For sample mean $\overline{X} = \dfrac{1}{n} \sum\limits_{i=1}^n X_i$,
\[\begin{align*} \text{Var}(\overline{X}) &= \text{Var}(\dfrac{1}{n} \sum\limits_{i=1}^n X_i) \\ &= \frac{1}{n^2} \left( \sum_{i=1}^n \text{Var}(X_i) + \sum_{i \ne j} \text{Cov}(X_i, X_j) \right) \\ &= \frac{1}{n^2} \big( n \sigma^2 + n(n-1) \rho \sigma^2 \big) \\ &= \rho \sigma^2 + \frac{1}{n} (1-\rho) \sigma^2 \\ &\lt \rho \sigma^2 + (1 - \rho) \sigma^2 \\ &= \sigma^2 \end{align*}\]where $\rho$ is the pairwise correlation, if $n \ge 2$ and $\rho \ne 1$ (multiple and different samples).
(assuming each pairwise correlation $\rho$ is same)
Thus by bagging, sampling and averaging, we obtain an ensemble model with lower variance and the same bias.
Choice of the sub-model
| Algorithm | Bias | variance |
|---|---|---|
| Decision Tree | low | high |
| Linear Regression | high | low |
Using Bagging together with Linear Regression is less effective. (Source)
Since Decision Tree has low bias, it is good choice for the sub-model of Bagging.
Strategy to lower variance
\[\begin{align} \text{Var}(\overline{X}) &= \rho \sigma^2 + \frac{1}{n} (1-\rho) \sigma^2 \\ &= \frac{1}{n} \sigma^2 + \rho \left(1 - \frac{1}{n} \right) \sigma^2 \end{align}\]Strategy 1
From the equation $(1)$, the more sub-model ($n$), the lower variance.
Strategy 2
From the equation $(2)$, the lower correlation between sub-models ($\rho$), the lower variance.
3. Advantages vs Disadvantages
- Advantages
(Strategy 2) Since a single model is never shown the complete dataset, it’s ability to memorise is significantly constrained. Thus we can avoid overfitting(reduce the variance).
(Strategy 2) Bagging is most effective when each sub-model is uncorrelated by learning relationships across different components of the data set.
You can extract prediction intervals.
(Source) Conor Mc., Why Bagging Works - Disadvantages
a loss of interpretability of a model
computationally expensive
Bagging reduces the variance while retaining the bias.
4. Random Forest : a representative bagging model
It builds a number of parallel decision trees on different samples and takes their majority vote for classification or average in case of regression. (Source) Sruthi E R, Understanding Random Forest
For not maximally correlated trees (Strategy 2),
(Source) Dr. Robert Kübler, Understanding the Effect of Bagging on Variance and Bias visually
- Use a random subset of the training samples (bootstrapping) for each tree.
- Use a random subset of features (learning different relationships) in each step of growing each tree.
- anything else can be added to lower correlation between sub-models.