Ⅲ. 간소화된 스타포스 모형ⓑ : Markov Reward Process
Table of contents
- 1. 문제 제기
- 2. Markov Reward Process(MRP)
- 3. 모델링 - absorbing MRP with zero discount factor
- 4. 3의 결과를 바탕으로 python 을 이용하여 강화비용의 기댓값 도출하기
- 5. ‘파괴복구비용 무시’ 가정의 파괴
메이플스토리 인게임 상의 스타포스는 등급상승, 등급유지, 등급하락, 파괴, 강화단계별 차등 강화비용, 파괴복구(장비흔적 전승), 파괴방지(12성~16성), 각종 이벤트 등 강화확률·강화(시도)비용 변화요소가 모두 존재하는 상당히 복잡한 시스템이다.
이 모형에서는 이 가운데 ①파괴복구(장비흔적 전승) 비용과 강화확률 변화요소 중 ②찬스타임을 무시한다.
즉 장비흔적 전승에 있어, 전승받을 장비아이템(소위 노작템)을 구하는데 드는 비용을 0 이라 가정한다. 또, 연속하여 실패하더라도 성공 확률 보정이 없다고 가정한다.
1. 문제 제기
장비 파괴 시 복구 비용과 찬스타임을 배제하였을 때, 각 강화 단계에서의 강화비용의 기댓값은 무엇인가.
2. Markov Reward Process(MRP)
Definition reward funtion $g$
\[g : S \rightarrow \mathbb{R}\](State) Reward $g(s)$ is the constant value that agent is anyway going to receive for being at the state $s \in S$.
For example, $g(X_i)$ is the reward receive by the agent in the i-th states in the stochastic process.
Definition Markov Reward Process $< S, P, g, \gamma>$
$S$ : finite set of states
$P$ : a transition matrix of given stochastic process with Markov property.
$g$ : a reward function
$\gamma$ : a discount factor, $\gamma \in [0, 1]$
3. 모델링 - absorbing MRP with zero discount factor
위 정의로부터 간소화된 스타포스 모형ⓑ는 absorbing MRP 에 해당함을 알 수 있다.
등급상승, 등급유지, 등급하락, 파괴, 파괴방지, 이벤트 등으로 인한 강화확률 변화는 transition matrix 로 모두 표현할 수 있고, 강화단계별 차등 강화비용, 이벤트 등으로 인한 강화(시도)비용 변화는 reward 로 모두 표현할 수 있다.
이때 discount factor $\gamma = 0$ 이다.
Definition recurrent state and $\tau_C$
Let $T_j(1)$ be the first visit time to state $j$.
A state $i \in S$ is recurrent if
where $ P_i(\cdot)=P(\cdot\vert X_0=i) $. Namely, we are sure agent will come back to the state eventually.
Let $\tau_C$ be the first visit time of the set $C$, then $X_{\tau_C}$ is the value of $X$ at (random) time $\tau_C$.
Definition expected total reward before absorption $v_i$
\[v_i = E_i[\sum_{n=0}^{\tau_C-1}g(X_n)]\]where $E_i[\cdot] = E[\cdot\vert X_0 = i]$ and $g(i)$ is reward for visiting state $i$.
Theorem solution of expected total reward
\[v_i = g(i) + \sum_{k \in T} p_{ik}v_k\]proof) Let $T$ be a set of transient state. Then
\[\begin{align*} v_i &= E_i[\sum_{n=0}^{\tau_C-1}g(X_n)] \\ &= g(i) + E_i[\sum_{n=1}^{\tau_C-1}g(X_n)] \\ &= g(i) + \sum_{k \in S}E_i[\sum_{n=1}^{\tau_C-1}g(X_n)\vert X_1=k]P_i(X_i=k) \quad \because \text{law of total probability} \\ &= g(i) + \sum_{k \in S}p_{ik}E_i[\sum_{n=1}^{\tau_C-1}g(X_n)\vert X_1=k] \\ &= g(i) + \sum_{k \in T}p_{ik}v_k \end{align*}\]since
\[E_i[\sum\limits_{n=1}^{\tau_C-1}g(X_n)\vert X_1=k] = \begin{cases} E_k[\sum\limits_{n=0}^{\tau_C-1}g(X_n)]=v_k & \quad \text{if } k \in T\\ 0 & \quad \text{if } k \notin T \end{cases}\]Corollary expected total reward vector $\mathbf{v}$
Let $T$ be a set of transient state.
Let vector $\mathbf{v}=(v_i)$ and $\mathbf{g}=(g_i)$ for $i \in T$. Then
where $N$ is the fundamental matrix.
sketch of proof) By the theorem, $\mathbf{v} = \mathbf{g} + Q\mathbf{v}$. $(I-Q)^{-1} = N$. ▨
위 정리에서는 reward function $g(\cdot)$ 가 state 방문 시 획득하는 reward 를 의미한다.
하지만 우리의 모형에서 구하고자 하는 강화(시도)비용은 state 를 떠날 때의 reward 에 해당한다.
그러나 이는 단순 표기의 차이로, expected total reward 의 정의를 위의 $v_i = E_i[\sum\limits_{n=0}^{\tau_C-1}g(X_n)]$ 에서 $ v_i = E_i[\sum\limits_{n=1}^{\tau_C}g(X_n)]$ 로 바꾸고 $g(\cdot)$ 가 state 를 떠날 때 획득하는 reward 를 의미하는 것으로 바꾸어 생각하면 문제없다.
4. 3의 결과를 바탕으로 python 을 이용하여 강화비용의 기댓값 도출하기
(1) 강화 확률표 만들기
GitHub Link : table.py
Output :
>>> StarForceTable(starcatch=True).prob_table
up keep down destroy
from
0 0.9975 0.00250 0.00000 0.00000
1 0.9450 0.05500 0.00000 0.00000
2 0.8925 0.10750 0.00000 0.00000
3 0.8925 0.10750 0.00000 0.00000
4 0.8400 0.16000 0.00000 0.00000
5 0.7875 0.21250 0.00000 0.00000
6 0.7350 0.26500 0.00000 0.00000
7 0.6825 0.31750 0.00000 0.00000
8 0.6300 0.37000 0.00000 0.00000
9 0.5775 0.42250 0.00000 0.00000
10 0.5250 0.47500 0.00000 0.00000
11 0.4725 0.00000 0.52750 0.00000
12 0.4200 0.00000 0.57420 0.00580
13 0.3675 0.00000 0.61985 0.01265
14 0.3150 0.00000 0.67130 0.01370
15 0.3150 0.66445 0.00000 0.02055
16 0.3150 0.00000 0.66445 0.02055
17 0.3150 0.00000 0.66445 0.02055
18 0.3150 0.00000 0.65760 0.02740
19 0.3150 0.00000 0.65760 0.02740
20 0.3150 0.61650 0.00000 0.06850
21 0.3150 0.00000 0.61650 0.06850
22 0.0315 0.00000 0.77480 0.19370
23 0.0210 0.00000 0.68530 0.29370
24 0.0105 0.00000 0.59370 0.39580
스타캐치(성공확률 변동요소)만 적용된 경우의 각 강화 단계 별 성공/유지/실패/파괴 확률이다.
(2) transition matrix $P$ 만들기
GitHub Link : starforce.py
Output (스타캐치만 적용된 경우, 일부만 표시) :
>>> starforce_transition_matrix_class = StarForceTransitionMatrix(absorbing_stage=18, starcatch=True)
>>> P = starforce_transition_matrix_class.transition_matrix
>>> pd.DataFrame(P)*100
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
0 0.25 99.75 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
1 0.00 5.50 94.50 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
2 0.00 0.00 10.75 89.25 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
3 0.00 0.00 0.00 10.75 89.25 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
4 0.00 0.00 0.00 0.00 16.00 84.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
5 0.00 0.00 0.00 0.00 0.00 21.25 78.75 0.00 0.00 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
6 0.00 0.00 0.00 0.00 0.00 0.00 26.50 73.50 0.00 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
7 0.00 0.00 0.00 0.00 0.00 0.00 0.00 31.75 68.25 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
8 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 37.00 63.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
9 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 42.25 57.75 0.00 0.000 0.00 0.00 0.000 0.000 0.0 0.0
10 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 47.50 52.50 0.000 0.00 0.00 0.000 0.000 0.0 0.0
11 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 52.75 0.00 47.250 0.00 0.00 0.000 0.000 0.0 0.0
12 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 57.42 0.580 42.00 0.00 0.000 0.000 0.0 0.0
13 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 63.250 0.00 36.75 0.000 0.000 0.0 0.0
14 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 1.370 67.13 0.00 31.500 0.000 0.0 0.0
15 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 2.055 0.00 0.00 66.445 31.500 0.0 0.0
16 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 2.055 0.00 0.00 66.445 0.000 31.5 0.0
17 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 2.055 0.00 0.00 0.000 66.445 0.0 31.5
18 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.000 0.00 0.00 0.000 0.000 0.0 100.0
(3) vector of reward function value $\mathbf{g}$ 만들기
GitHub Link : starforce.py
Output :
>>> cost160 = StarForceCost(item_lv=160, mvp="bronze", pc_room=False, event30=True,
prevent1216=(False, False, False, False, False)).reward
>>> df = pd.DataFrame(cost160, columns=["cost"])
>>> df.index.name = "from"
>>> df
cost
from
0 90400
1 180200
2 270000
3 359800
4 449500
5 539300
6 629100
7 718900
8 808600
9 898400
10 3638100
11 4601400
12 5711300
13 6976300
14 8404600
15 20008000
16 23566200
17 28946000
18 33495400
19 38470700
20 43887500
21 49761000
22 56106400
23 62938600
24 70272300
인게임에서 가장 자주 강화되는 상황에 대한 reward vector 를 대표적으로 제시한다.
강화 대상 아이템의 레벨은 160, 비용변동요소는 비용 30% 할인 이벤트만 적용된 경우이다.
(4) fundamental matrix $N$ 을 구하여 expected total reward $\mathbf{v}$ 구하기
GitHub Link : calculator.py
Output :
>>> StarForceCalculator(goal=22, item_lv=160, base_price=0,
... starcatch=True, mvp="bronze", pc_room=False,
... event30=True, event51015=False, event1plus1=False,
... prevent1216=(False, False, False, False, False)).print_interval_cost()
Expected Interval Cost cumulative
from
0 115,689 115,689
1 243,492 359,181
2 386,331 745,512
3 514,846 1,260,358
4 683,452 1,943,810
5 874,667 2,818,477
6 1,093,197 3,911,674
7 1,345,348 5,257,022
8 1,639,524 6,896,546
9 1,987,186 8,883,732
10 8,852,571 17,736,303
11 22,323,453 40,059,756
12 47,890,778 87,950,534
13 106,674,604 194,625,137
14 268,142,562 462,767,699
15 108,720,153 571,487,853
16 359,573,819 931,061,672
17 928,122,266 1,859,183,938
18 2,224,851,125 4,084,035,063
19 5,144,622,614 9,228,657,678
20 2,167,244,310 11,395,901,987
21 6,902,770,190 18,298,672,177
Expected Interval Cost 는 각 강화 단계에서 시작하여 바로 다음 강화 단계에 도달하기까지 드는 비용의 기댓값을 의미한다.
cumulative 는 Expected Interval Cost 열의 누적합으로서, 강화 0단계에서 시작하여 각 열 다음 강화 단계에 도달하기까지 드는 비용의 기댓값을 의미한다.
아이템 레벨은 160, 스타캐치 및 강화비용 30% 할인 이벤트가 적용된 경우를 나타내었다.
(5) 반복 simulation 을 통해 얻은 실험적 평균비용과의 비교
GitHub Link : simulation.py
Output :
>>> simulator = StarforceSimulatorVer2(start=0, goal=22, item_lv=160, base_price=0, starcatch=True, event30=True)
>>> simulator.realtime_reduced_mean(iteration=3000)
>>> simulator.draw_mean_graph(guide_line=True)
 |
|---|
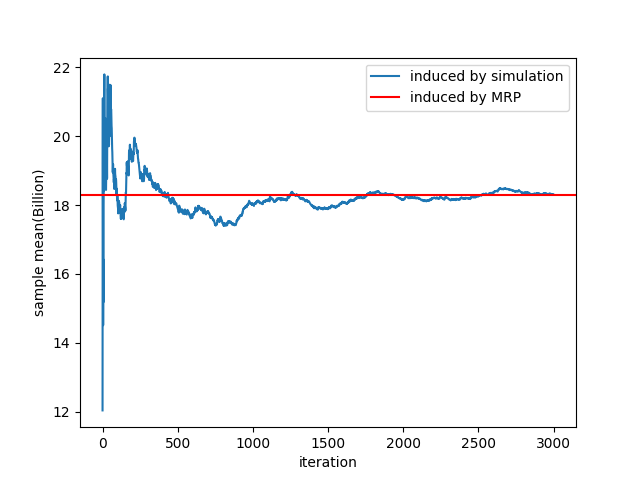
| 반복 시뮬레이션으로 구한 누적 평균비용(blue) / MRP 로 구한 기대비용(red) |
①아이템 레벨 160, ②강화단계 0단계 -> 22단계, ③스타캐치 적용, ④30% 강화비용 할인 적용, ⑤장비 파괴복구 비용 무시
이상의 조건 하에서 시뮬레이션으로 도출한 평균 강화비용과 MRP model 로 도출한 기대 강화비용이 거의 일치함을 위 그래프에서 확인할 수 있다.
이를 통해 MRP 를 통해 기대 강화비용을 도출한 결과가 타당함을 알 수 있다.
5. ‘파괴복구비용 무시’ 가정의 파괴
GitHub Link : simulation.py
Output:
>>> simulator = StarforceSimulatorVer2(start=0, goal=22, item_lv=160,
base_price=100000000, starcatch=False, event30=True)
>>> simulator.realtime_reduced_mean(iteration=3000)
>>> simulator.draw_mean_graph(guide_line=True)
 |
|---|
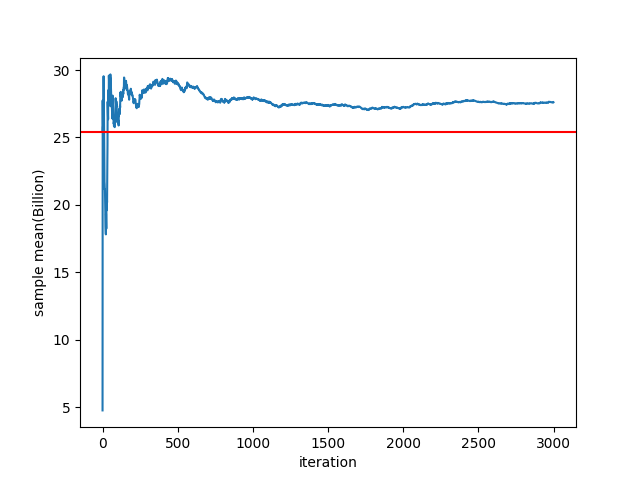
| 반복 시뮬레이션으로 구한 누적 평균비용(blue) / MRP 로 구한 기대비용(red) |
이제 장비 파괴복구 비용을 복구 1회당 100,000,000 이라고 가정하면 위 그림에서 MRP model 에서의 기대 강화비용이 실제 평균 강화비용보다 과소평가됨을 확인할 수 있다. (blue line 과 red line 의 차이)
이 두 값의 차이는 강화 과정 중 평균 파괴횟수와 밀접한 관련이 있을 것이다.
파괴복구비용을 모형ⓒ에서 명시적으로 고려하여 평균 강화비용을 구해보자.